PENGERTIAN TURUNAN DAN SIFAT-SIFATNYA BERSAMA CONTOH SOALNYA

Nadia Nur Anggraini (28)
XI IPS 3



        TURUNAN DAN SIFAT-SIFATNYA 

DEFINISI TURUNAN

Turunan merupakan suatu perhitungan terhadap perubahan nilai fungsi karena perubahan nilai input (variabel).

Turunan dapat disebut juga sebagai diferensial dan proses dalam menentukan turunan suatu fungsi disebut sebagai diferensiasi.

Menggunakan konsep limit yang sudah dipelajari, turunan dapat didefinisikan sebagai

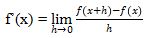
Rumus Turunan

turunan tersebut didefinisikan sebagai limit dari perubahan rata-rata dari nilai fungsi terhadap variabel x.

Penerapan Turunan

Berikut merupakan beberapa penerapan turunan.

  • Turunan dapat diterapkan untuk menghitung gradien dari garis singgung suatu kurva.
  • Turunan dapat digunakan untuk menentukan interval dimana suatu fungsi naik atau turun.
  • Turunan dapat diterapkan untuk menentukan nilai stasioner suatu fungsi.
  • Turunan dapat diterapkan dalam menyelesaikan permasalahan yang berkaitan dengan persamaaan gerak.
  • Turunan dapat digunakan untuk menyelesaikan permasalahan maksimum-minimum.

Berikut ini akan dijelaskan mengena rumus turunan.

Rumus Turunan

Berikut merupakan beberapa rumus dasar untuk menentukan turunan.

  • f(x) = c, dengan c merupakan konstanta

Turunan dari fungsi tersebut adalah f’(x) = 0.

  • f(x) = x

Turunan dari fungsi tersebut adalah f’(x) = 1.

  • f(x) = axn

Turunan dari fungsi tersebut adalah f’(x) = anxn – 1

  • Penjumlahan fungsi:  h(x) = f(x) + g(x)

Turunan fungsi tersebut yaitu h’(x) = f’(x) + g’(x).

  • Pengurangan fungsi: h(x) = f(x) – g(x)

Turunan fungsi tersebut adalah h’(x) = f’(x) – g’(x)

  • Perkalian konstanta dengan suatu fungsi (kf)(x).

Turunan fungsi tersebut adalah k . f’(x).

SIFAT - SIFAT TURUNAN

  1. Aturan Konstanta

    Jika f(x) = k dengan k suatu konstanta maka untuk sebarang x, f'(x) = 0 yakni Dx(k) = 0

  2. Aturan Fungsi Identitas
    Jika f(x) = x maka f'(x) = 1 yakni Dx(x) = 1

  3. Aturan Pangkat

    Jika f(x) = xn, dengan n bilangan-bilangan bulat positif maka f(x) = nxn-1 yakni Dx(xn) = nxn-1

  4. Aturan Kelipatan Konstan

    Jika k suatu konstanta dan f suatu fungsi yang terdiferensial maka (kf)’ = k f'(x) yakni Dx[k f(x)] = k Dx[f(x)]

  5. Aturan Jumlah

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f + g)(x) = f(x) + g(x) yakni Dx[f(x) + g(x)] = Dx[f(x)] + Dx[g(x)]

  6. Aturan Selisih

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f – g)(x) = f(x) – g(x) yakni Dx[f(x) – g(x)] = Dx[f(x)] – Dx[g(x)]

  7. Aturan Hasil Kali

    Jika f dan g fungsi-fungsi yang terdiferensial maka (f . g)'(x) = f'(x)g(x) + f(x)g'(x) yakni Dx[f(x)g(x)] = Dx[f(x)]g(x) + f(x)Dx[g(x)]

  8. Aturan Hasil Bagi

    Jika f dan g fungsi-fungsi yang terdiferensial maka \left ( \frac{f}{g} \right )(x)= \frac{f'(x)g(x)-f(x)g'(x)}{g^2(x)} yakni Dx \frac{f(x)}{g(x)}= \frac{D_x[f(x)]g(x)-f(x)D_x[g(x)]}{g^2(x)}


CONTOH SOAL 1
Tentukan turunan pertama dari fungsi f(x) = x3 – 2x2 + 3x !

Pembahasan :

f’(x) = 3.1.x3-1 – 2.2x2-1 + 1.3.x1-1

f’(x) = 3x2 – 4x + 3

Jadi, turunan pertama dari fungsi f(x) = x3 – 2x2 + 3x adalah f’(x) 3x2 – 4x + 3.


CONTOH SOAL 2

Carilah turunan pertama dari fungsi f(x) = (3x + 2)(2x + 5) !

Pembahasan :

f(x) = (3x + 2)(2x + 5)

f(x) = 3x.2x + 3x.5 + 2.2x + 2.5

f(x) = 6x2 + 15x + 4x + 10

f(x) = 6x2 + 19x + 10

f’(x) = 2.6.x2-1 + 1.19.x1-1 + 0.10.x0-1

f’(x) = 12x + 19 + 0

f’(x) = 12x + 19

Jadi turunan pertama dari fungsi f(x) = (3x + 2)(2x + 5) adalah f’(x) = 12x + 19 + 0 .


CONTOH SOAL 3

Hitunglah turunan pertama dari fungsi f(x) = 4x½ !

Pembahasan :

f’(x) = ½.4.x½-1

f’(x) = 2x-½

Jadi turunan pertama dari fungsi f(x) = 4x½ adalah f’(x) = 2x-½ .



CONTOH SOAL 4

Tentukan turunan pertama dari fungsi f(x) = (x2 + 3x + 4)(2x + 3).


Pembahasan :

f(x) = (x2 + 3x + 4)(2x + 3)

Misal:

u = x2 + 3x + 4

v = 2x + 3

Maka:

u’ = 2x + 3

v’ = 2

Sehingga:

f’(x) = u’v + uv’

f’(x) = (2x + 3)(2x + 3) + (x2 + 3x + 4).2

f’(x) = 4x2 + 12x + 9 + 2x2 + 6x + 8

f’(x) = 6x2 + 18x + 17

Jadi, turunan dari f(x) = (x2 + 3x + 4)(2x + 3) adalah f’(x) = 6x2 + 18x + 17.



CONTOH SOAL 5

Carilah turunan pertama dari f(x) = (x3+4) / (2x+3) !


Pembahasan :

Misal:

u = x3+4

v = 2x+3

Maka:

u’ = 3x2

v’ = 2

Sehingga

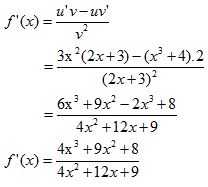
Contoh Soal Turunan 6

Jadi,  turunan pertama dari f(x) = (x3+4) / (2x+3) adalah f’(x) = (4x3 + 9x2 + 8) / (4x2 + 12x + 9).


DAFTAR PUSTAKA

https://rumuspintar.com/turunan/

https://gurubelajarku.com/contoh-soal-turunan/

https://aimprof08.wordpress.com/2012/05/02/turunan-dan-sifat-sifatnya/

Komentar

Posting Komentar

Postingan populer dari blog ini

TRIGONOMETRI

Gambar
NADIA NUR ANGGRAINI (28) X IPS 3 Materi matematika yang saya sukai di semester 2 ini adalah tentang aturan sinus dan cosinus. Karena materi ini rumusnya tidak terlalu rumit jika kita dapat memahami rumusnya dengan baik kita pasti dapat mengerjakannya. Walaupun  materi tersebut dilihatnya sedikit susah, tetapi jika kita memiliki usaha untuk terus mencoba pasti bisa mengerjakannya dengan baik dan benar SOAL DAN PEMBAHASAN TRIGONOMETRI 3.7 Menyelesaikan Cara Mengubah Satuan Pengukuran Sudut Trigonometri Radian ke Derajat, Derajat ke Radian Contoh soal 1 :  Nyatakan besar sudut berikut ke dalam satuan radian! a. 30° 20′ 15” b. 106° 20′ Penyelesainnya : a. kita ketahui bahwa: 1” = (1/3600)° 1′ = (1/60)° 1° = 0,0174 radian, maka: 30° 20′ 15” = 30° + 20.(1/60)° + 15.(1/3600)° = (108000/3600)° + (1200/3600)° + (15/3600)° = (109215/3600)° = (109215/3600).0,0174 radian = 0,53 rad b. kita ketahui bahwa: 1′ = (1/60)° 1° = 0,0174 radian, maka: 106° 20′ = 106° + 20...
Baca selengkapnya

SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN TURUNAN

Nadia Nur Anggraini / 28 XI IPS 3 SOAL KONTEKSTUAL YANG BERHUBUNGAN DENGAN TURUNAN Contoh soal 1 Suatu perusahaan memproduksi  x x  unit barang dengan biaya  ( 4 x 2 − 8 x + 24 ) ( 4 x 2 − 8 x + 24 )  ribu rupiah untuk tiap unit. Jika barang tersebut terjual habis dengan harga Rp40.000,00 untuk tiap unit, maka keuntungan maksimum yang diperoleh perusahaan tersebut adalah  ⋯ ⋅ ⋯ ⋅ A. Rp16.000,00                    D. Rp52.000,00 B. Rp32.000,00                     E. Rp64.000,00 C. Rp48.000,00 Pembahasan   Misalkan  f ( x ) f ( x )  menyatakan total biaya produksi  x x  unit barang,  g ( x ) g ( x )  menyatakan harga jual  x x  unit barang dalam satuan ribu rupiah, dan  h ( x ) h ( x )  menyatakan keuntungan yang diperoleh atas penjualan  x x  unit barang, maka f ( x ) = x ( 4 x 2 − 8 x + 24 ) = 4 x 3 ...
Baca selengkapnya

SOAL TRANSFORMASI DAN PENYELESAIANNYA

Gambar
Nama : Nadia Nur Anggraini No absen : 28 Kelas : XI IPS 3 SOAL TRANSFORMASI DAN PENYELESAIANNYA Contoh soal 1 : Jika transformasi T1, memetakan (x, y) ke (-y, x) dan transformasi T2 menyatakan (x, y) ke (-y, -x) dan jika transformasi T merupakan transformasi T1 yang diikuti oleh transformasi T2, maka matriks T adalah ... Pembahasan : Rotasi +90^0 yang berpusat di titik O(0, 0) memiliki matriks:  -    T1 merupakan rotasi +90^0 dengan pusat O(0,0) maka matriksnya adalah:  -    T2 merupakan pencerminan y = -x, maka matriksnya:  Contoh soal 2 : Bayangan kurva y = 3x – 9x^2 jika di rotasi dengan pusat O (0, 0) sejauh 90^0 dilanjutkan dengan dilatasi dengan pusat O (0, 0) dan faktor skala 3 adalah ... Pembahasan : -    Rotasi dengan pusat O(0, 0) sejauh 90^0 memiliki matriks: -    Dilatasi dengan pusat O(0, 0) dan faktor skala 3 memiliki matriks:  T1 =  dan T2 =  T2 o T1 =  Maka matriks transformasi...
Baca selengkapnya

DAERAH BERSIH DAN DAERAH KOTOR PROGRAM LINIER

Gambar
Nama : Nadia Nur Anggraini (28) Kelas : XI IPS 3  Daerah Bersih dan Daerah Kotor Program Linier Gambar daerah bersih dan daerah kotor dari pertidaksamaan  3x + 2y ≤ 12, 5x + 3y < 19, x ≥ 0, y > 0 PENYELESAIAN: 3x + 2y ≤ 12  x = 0 3.0 + 2y = 12          2y = 12             y = 6 3x + 2.0 = 12          3x = 12             x = 4 5x + 3y < 19    y = 0  5x + 3.0 = 19           5x = 19              x = 3,8  5.0 + 3y = 19           3y = 19              y = 6,3 DAERAH PENYELESAIAN daerah penyelesaian x ≥ 0 daerah penyelesaian y > 0   DAERAH ARSIRAN gambar daerah kotor gambar daerah bersih KESIMPULAN: Daerah kotor - Himpunan/daerah penyelesaiannya adalah daerah yang mengalami banyak arsiran Dae...
Baca selengkapnya

LOGIKA TRIGONOMETRI

Gambar
Juli, 13 2020 Nadia Nur Anggraini (28) XI IPS 3 LOGIKA MATEMATIKA A. Pengertian Logika matematika   adalah gabungan dari ilmu logika dan ilmu matematika. Logika berasal dari bahasa yunani kuno yaitu   λόγος (logos) , logos dapat diartikan sebagai hasil pertimbangan akal atau pikiran yang dinyatakan lewat kata atau bahasa. Sedangkan jika diartikan secara sistematis, logika dapat dianalisis berdasarkan nilai-nilai kebenaran. Logika matematika diartikan sebagai cabang logika dan matematika yang mengandung kajian logika matematis dan aplikasi kajian ini pada bidang-bidang lain di luar matematika. Logika matematika berhubungan erat dengan ilmu komputer dan logika filosofis. Logika matematika memiliki kegunaan yaitu untuk menganalisis kasus atau sebagai media penarik kesimpulan. Logika matematika sebagai ilmu independen yang muncul pada abad pertengahan ke 19. Pada abad sebelumnya, logika matematika ini dipelajari melalui Ilmu Retorika, Silogisme, & sebagai Ilmu Filsafat. S...
Baca selengkapnya