TRIGONOMETRI

NADIA NUR ANGGRAINI (28)
X IPS 3



Materi matematika yang saya sukai di semester 2 ini adalah tentang aturan sinus dan cosinus. Karena materi ini rumusnya tidak terlalu rumit jika kita dapat memahami rumusnya dengan baik kita pasti dapat mengerjakannya. Walaupun  materi tersebut dilihatnya sedikit susah, tetapi jika kita memiliki usaha untuk terus mencoba pasti bisa mengerjakannya dengan baik dan benar

SOAL DAN PEMBAHASAN TRIGONOMETRI

3.7 Menyelesaikan Cara Mengubah Satuan Pengukuran Sudut Trigonometri Radian ke Derajat, Derajat ke Radian

Contoh soal 1 : 
Nyatakan besar sudut berikut ke dalam satuan radian!
a. 30° 20′ 15”
b. 106° 20′
Penyelesainnya :

a. kita ketahui bahwa:

1” = (1/3600)°
1′ = (1/60)°
1° = 0,0174 radian, maka:
30° 20′ 15”
= 30° + 20.(1/60)° + 15.(1/3600)°
= (108000/3600)° + (1200/3600)° + (15/3600)°
= (109215/3600)°
= (109215/3600).0,0174 radian
= 0,53 rad

b. kita ketahui bahwa:

1′ = (1/60)°
1° = 0,0174 radian, maka:
106° 20′ = 106° + 20.(1/60)°
106° 20′ = (318/3)° + (1/3)°
106° 20′ = (319/3)°
106° 20′ = (319/3).0,0174 radian
106° 20′ = 1,85 rad.

Contoh soal 2 :Nyatakan sudut 50° dan 89° ke dalam radian!Penyelesaian:50° = 50° x π/180°50° = 0,277π50° = 0,277 (3,14)50° = 0,87 radian89° = 89° x π/180°89° = 0,494π89° = 0,494 (3,14)89° = 1,55 radian

Contoh Soal 3 :
Nyatakan sudut 0,45 radian dan 0,89 radian ke dalam satuan derajat!

Penyelesaian:

0,45 radian = 0,45 x 180°/π
0,45 radian = 25,80°
0,89 radian = 0,89 x 180°/π
0,89 radian = 51,02°

3.7 Menyelesaikan Rasio Trigonometri (sinus, cosinus, tangen, cosecan, secan dan cotangen) pada segitiga siku-siku dan sudut istimewa (60⁰ , 30⁰ , 45⁰ )

Contoh soal 1 :

Diketahui sebuah segitiga siku-siku ABC yang siku-siku di C, panjang sisi depan = a = 4 dan panjang sisi samping = b = 3. Tentukanlah perbandingan sudut sin, cos, dan tan!

Penyelesainnya :Berdasarkan soal di atas, sisi miring = cc2 = a2 + b2c2 = 42 + 32c2 = 16 + 9 = 25c = √25 = 5Sin a = 4/5 = 0,8Cos a = 3/5 = 0,6Tan a = 4/3

Contoh soal 2 :
Tentukan hasil dari: 2 cos 75° cos 15°

Penyelesainnya :
Menggunakan rumus trogonomteri sudut rangkap diperoleh sebagai berikut
2 cos 75° cos 15° = cos [75 +15]° + cos [75 – 15]
= cos 90° + cos 60°
= 0 + ½
= ½

3.7 Menyelesaikan rasio trigonometri (sinus, cosinus, tangen, cosecan, secan, dan cotangen) pada segitiga siku-siku di dalam koordinat kartesius

Contoh soal 1 :

Besar sudut yang sesuai dengan gambar di bawah adalah $\cdots \cdot$

Sudut yang terbentuk searah dengan jarum jam, sehingga tandanya negatif, yakni $-{30}^{\circ }$.
Karena satu putaran sama dengan ${360}^{\circ }$, maka $-{30}^{\circ }$ sama dengan $(360-30{)}^{\circ }={330}^{\circ }$

Contoh soal 2 :

Besar sudut ${72}^{\circ }$ sama dengan... rad

Penyelesaiannya :

Ingat bahwa $1^{\circ }=\frac{\pi }{180}\text{rad}$
Dengan demikian,
$\begin{array}{cc}{72}^{\circ }& ={72}^2\times \frac{\pi }{{180}^5}\text{rad}\\ & =\frac{2}{5}\pi \text{rad}\end{array}$
Jadi, besar sudut ${72}^{\circ }$ sama dengan 2/5π rad

3.7 Menyelesaikan nilai trigonometri pada suatu sudut segitiga siku-siku pada koordinat cartesius 

 Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya

v sin 20°pembahasan :sin 20° = sin (90° − 70°)            = cos 70°

v tan 40°

pembahasan :
tan 40° = tan (90° − 50°)
            = cot 50°
o   Nyatakan tiap perbandingan trigonometri berikut di dalam sudut 37° !
v tan  143°
pembahasan :

Sudut 143° adapada kuadran II, sampai tan 143° mempunyai nilai negatif.
tan 143° = tan (180° − 37°)
              = -tan 37°

v sin 233°
pembahasan :
Sudut 233° ada pada kuadran III, sehingga sinus mempunyai nilai negatif.
sin 233° = sin (270° − 37°
              = -cos 37°

3.7 Menyelesaikan komposisi operasi (+, -, :, dan •) nilai trigonometri

Contoh Soal 1 :

nilai dari sin 30° . cos 60° + sin 60° . cos 30°

Pembahasan :
sin 30° . cos 60° + sin 60° . cos 30°
1/2   . 1/2 + 1/2  . 1/2
1/4  + 1/4 .
1/4 + 1/4 . 3
1/4 + 3/4
4/4 = 1

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut di berbagai kuadran

Jika sin a = 1/2 , a di kuadran II , maka nilai dari tan a

Pembahasan :

Jadi tan A adalah : -1/3

3.8 Menyelesaikan rasio trigonometri untuk sudut-sudut berelasi (kuadrat: I, II, III, IV), sudut negatif, dan sudut > 360⁰

Contoh Soal 1

Untuk perbandingan trigonometri berikut, nyatakanlah dalam perbandingan trigonometri sudut komplemennya
sin 20°
tan 40°
cos 53°

Penyelesainnya :

sin 20° = sin (90° − 70°)
= cos 70°
tan 40° = tan (90° − 50°)
= cot 50°
cos 53° = cos (90° − 37°)
= sin 37°
Jika diperhatikan pada sin yang berubah menjadi cos, kemudian tan berubah jadi cot sedangkan cos berubah menjadi sin karena relasi yang dipaka adalah (90° − α) dan ketiga perbandingan trigonometri bernilai positif, karena sudut 20°, 40° dan 53° berada di kuadran I.

3.8 Menyelesaikan persamaan trigonometri sederhana atau persamaan indentitas trigonometri = rumus identitas trigonometri

Contoh soal :Nilai x yang memenuhi persamaan sin x 1/2 √3 persamaan trigono untuk  0°≤x≤360° adalah…….

Pembahasan : 
Kemungkinan 1
x=60°+k.360°
untuk k=0 ,diperoleh x=60° (benar)
untuk k=1 ,diperoleh x=420° (salah)
kemungkinan 2
x=(180°-60°) + k.360°
x=120° + k.360°
untuk k=0 ,diperoleh x=120° (benar)
untuk k=1 ,diperoleh x=480° (salah)
jadi nilai x yang memenuhi persamaan tersebut bila dinyatakan dalam notasi himpunan adalah {60°,120°}.

3.8 Menyelesaikan Koordinat kutub ke koordinat kartesius, koordinat kartesius ke koordinat kutub

Contoh Soal 1 :

Jika diketahui koordinat kartesius titik P(5, -5) maka koordinat kutubnya adalah . . .

Penyelesaian :
x = 5 dan y = -5  berada di Kuadran IV (270º – 360º)r² = x² + y² r² = 5² + (-5)²r² = 25 + 25r² = 50r = √50r = √25√2r = 5√2Tan θ = y/xTan θ = -5/5 = -1Tan yang bernilai 1 adalah sudut 45º.45º di Kuadran IV sma dengan sudut 360º – 45º = 315ºSehingga koordinat kutub yang dimaksud adalah P( 5√2, 315º)

Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar  dan , maka panjang BC = … cm.

Contoh soal 2 :

Jika diketahui koordinat kutub titik P( 5√2, 315º) maka koordinat kartesiusnya adalah . . .

Penyelesainnya :r = 5√2 dan θ = 315º
x = r.Cos θx = 5√2.Cos 315º
x = 5√2 × ½√2 = 5
y = r.Sin θy = 5√2.Sin 315º
y = 5√2 × (-½√2) = -5
Sehingga koordinat kartesius yang dimaksud adalah P( 5, -5)

3.8 Menyelesaikan soal cerita perbandingan trigonometri

Contoh soal 1 :

Seorang anggota pramuka berdiri 15 m dari kaki sebuah pohon besar yang tumbuh tegak lurus seperti ditunjukan pada gambar. jika sudut elevasi ke puncak pohon adalah 60᠐. berapakah tinggi pohon tersebut?

Penyelesaiannya :

Tinggi pohon Y dapat anda hitung dengan menggunakan perbandingan tangen

3.9 Menyelesaikan aturan sinus diketahui 2 sudut dan 1 sisi

Contoh soal 1 :

Suatu segitiga ABC memiliki panjang AC = 8 cm. Jika besar  dan 

maka panjang BC = … cm.

Penyelesaiannya :
Panjang BC dapat dicari menggunakan aturan sinus.

  

  

  

  

  

  

  

3.9 Menyelesaikan aturan sinus diketahui 1 sudut dan 2 sisi

Contoh Soal 1 :Diketahui suatu taman di tengah kota berbentuk segitiga sembarang. Jika sudut apit sebesar 60o dan dua sisi yang mengapitnya masing-masing panjangnya 18 meter dan 16 meter, maka luas taman tersebut adalah..

Penyelesaiannya :
Untuk menentukan luas segitiga sembarang yang diketahui panjang dua sisi dan sudut antara kedua sisi tersebut dapat memanfaatkan fungsi sinus.

  

  

  

3.9 Menyelesaikan aturan cos ditanya sisi

Contoh soal 1 :Diketahui sebuah segitiga ABC memiliki sisi dengan panjang
a = 10 cm
c = 12 cm
besar sudut B = 60̊.
Hitung panjang sisi b!

Penyelesaiannya :b2 = a2+ c2 – 2ac cos B
b2 = 100+144 – 44 cos 60̊
b2 = 244 – 44(0,5)
b2 = 244 – 22
b2 = 222
b = 14,8997
Jadi, panjang sisi b adalah 14,8997cm

3.9 Menyelesaikan Luas segitiga jika diketahui: 1 sudut 2 sisi, 3 sisi, 2 sudut 1 sisi

Contoh soal 1 :

Diketahui sebuah segitiga siku-siku dengan panjang alasnya 8 cm dan tinggi 6 cm. Hitunglah keliling dan luas segitiga tersebut!
Penyelesaiannya :Karena segitiga tersebut merupakan segitiga sama sisi, sehingga ketiga sisinya sama panjang.a = 6 cmt = 8 cmUntuk menghitung keliling segitiga tersebut, kita mencari sisi miringnya terlebih dahulu dengan dalil phytagoras. Misalkan sisi miring kita simbolkan dengan c, sehinggac² = a² + b²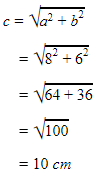

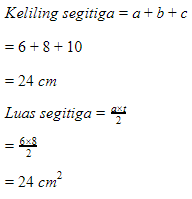
3.10 Menyelesaikan membaca gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x
 

Diketahui f(x) = sin(cos x)

jawab : f"(x) = - (cos x) . (cos (cos x)) – (sin x) . (sin x) . (sin (cos x))

 

Temukan turunan pertama dari f (x) = tan x + Sec x

jawab : f''(x) = sec 2x + Sec  x tan x = Sec x ( Sec x + tan x)

3.10 Menyelesaikan gambar fungsi trigonometri f(x) = sin x, f(x) = cos x, f(x) = tan x, f(x) = csc x, f(x) = sec x, f(x) = cot x

Grafik di atas merupakan modifikasi grafik cosinus (karena tidak dimulai dari garis normal di sumbu-$X$) dengan bentuk umum $f\left(x\right)=a\cos kx$.

Grafik juga menunjukkan bahwa nilai maksimum fungsinya $\frac{1}{2}$, sedangkan nilai minimumnya $-\frac{1}{2}$, sehingga
$\begin{array}{cc}a& =\frac{\text{N. Maksimum}-\text{N. Minimum}}{2}\\ & =\frac{\frac{1}{2}-(-\frac{1}{2})}{2}=\frac{1}{2}\end{array}$
Saat $x=0^{\circ }$, nilai fungsinya $\frac{1}{2}$, lalu berulang kembali di $x=\pi$, sehingga periodenya $\pi$. 
Dengan demikian, 
$k=\frac{2\pi }{\text{Periode}}=\frac{2\pi }{\pi }=2$

.

Grafik fungsi di atas adalah grafik fungsi 

$f\left(x\right)=\frac{1}{2}\cos 2x$

3.10 Menyelesaikan fungsi trigonometri dengan menggunakan lingkaran satuan untuk

menentukan periode maksimum dan minimum

contoh soal :

Nilai minimum dari fungsi y = √3 cos x - sin x adalah...

Pembahasan : 

Nilai Maksimum minimum fungsi trigonometri

y = √3 cos x - sin x  ubah  bentu ke y = k  cos ( x -  a)
a= √3
b = - 1
k = √(a²+b²)
k = √(3 +1)= +_2

Jadi, nilai minimum nya adalah = -2

Terima Kasih