SOAL TRANSFORMASI DAN PENYELESAIANNYA
Nama : Nadia Nur Anggraini
No absen : 28
Kelas : XI IPS 3
SOAL TRANSFORMASI DAN PENYELESAIANNYA
Contoh soal 1 :
Jika transformasi T1, memetakan (x, y) ke (-y, x) dan transformasi T2 menyatakan (x, y) ke (-y, -x) dan jika transformasi T merupakan transformasi T1 yang diikuti oleh transformasi T2, maka matriks T adalah ...
Pembahasan :
Rotasi +90^0 yang berpusat di titik O(0, 0) memiliki matriks: 
- T1 merupakan rotasi +90^0 dengan pusat O(0,0) maka matriksnya adalah:
- T2 merupakan pencerminan y = -x, maka matriksnya:


- T1 merupakan rotasi +90^0 dengan pusat O(0,0) maka matriksnya adalah:

- T2 merupakan pencerminan y = -x, maka matriksnya:

Contoh soal 2 :
Bayangan kurva y = 3x – 9x^2 jika di rotasi dengan pusat O (0, 0) sejauh 90^0 dilanjutkan dengan dilatasi dengan pusat O (0, 0) dan faktor skala 3 adalah ...
Pembahasan :
- Rotasi dengan pusat O(0, 0) sejauh 90^0 memiliki matriks:
- Dilatasi dengan pusat O(0, 0) dan faktor skala 3 memiliki matriks:
T1 = dan T2 =
dan T2 = 
T2 o T1 =
Maka matriks transformasinya adalah:

Dari matriks transformasi di atas didapatkan:
x’ = -3y, maka y = -1/3 x’ dan
y’ = 3x, maka x = 1/3y’
Jadi, bayangan kurva y = 3x – 9x^2 menjadi:
y = 3x – 9x^2
-1/3x’ = 3(1/3y’) – 9(1/3y’)^2
-1/3x’ = y’ - y’^2 (hasil perkalian 3)
-x’ = 3y’ – 3y’^2
x’ = 3y’^2 – 3y’ (hasil perkalian -)
Jadi, bayangannya adalah x = 3y^2 – 3y

- Dilatasi dengan pusat O(0, 0) dan faktor skala 3 memiliki matriks:

T1 =
 dan T2 =
dan T2 = 
T2 o T1 =
Maka matriks transformasinya adalah:

Dari matriks transformasi di atas didapatkan:
x’ = -3y, maka y = -1/3 x’ dan
y’ = 3x, maka x = 1/3y’
Jadi, bayangan kurva y = 3x – 9x^2 menjadi:
y = 3x – 9x^2
-1/3x’ = 3(1/3y’) – 9(1/3y’)^2
-1/3x’ = y’ - y’^2 (hasil perkalian 3)
-x’ = 3y’ – 3y’^2
x’ = 3y’^2 – 3y’ (hasil perkalian -)
Jadi, bayangannya adalah x = 3y^2 – 3y
Contoh soal 3 :
Persamaan bayangan garis 2y – 5x – 10 = 0 oleh rotasi (0, 90^0) dilanjutkan refleksi terhadap garis y = -x adalah ...
Pembahasan :
T1 adalah rotasi dengan pusat O (0, 0), memiliki matriks: 
T2 adalah refleksi terhadap garis y = -x, memiliki matriks:
T2 o T1 =
Maka:

Dari transformasi di atas, didapatkan:
x’ = -x, sehingga x = -x’
y’ = y, sehingga y = y’
Jadi, bayangan garis 2y – 5x – 10 = 0 adalah:
2y – 5x – 10 = 0
2y’ – 5(-x’) – 10 = 0
2y’ + 5x’ – 10 = 0 atau 2y + 5x – 10 = 0

T2 adalah refleksi terhadap garis y = -x, memiliki matriks:

T2 o T1 =

Maka:

Dari transformasi di atas, didapatkan:
x’ = -x, sehingga x = -x’
y’ = y, sehingga y = y’
Jadi, bayangan garis 2y – 5x – 10 = 0 adalah:
2y – 5x – 10 = 0
2y’ – 5(-x’) – 10 = 0
2y’ + 5x’ – 10 = 0 atau 2y + 5x – 10 = 0
Contoh soal 4 :
Diketahui translasi  Titik-titik A’ dan B’ berturut-turut adalah bayangan titik-titik A dan B oleh komposisi transformasi T1 o T2. Jika A(-1, 2), A’(1, 11), dan B’(12, 13) maka koordinat titik B adalah...
Titik-titik A’ dan B’ berturut-turut adalah bayangan titik-titik A dan B oleh komposisi transformasi T1 o T2. Jika A(-1, 2), A’(1, 11), dan B’(12, 13) maka koordinat titik B adalah...
 Titik-titik A’ dan B’ berturut-turut adalah bayangan titik-titik A dan B oleh komposisi transformasi T1 o T2. Jika A(-1, 2), A’(1, 11), dan B’(12, 13) maka koordinat titik B adalah...
Titik-titik A’ dan B’ berturut-turut adalah bayangan titik-titik A dan B oleh komposisi transformasi T1 o T2. Jika A(-1, 2), A’(1, 11), dan B’(12, 13) maka koordinat titik B adalah...Pembahasan :
Titik A(-1, 2) memiliki bayangan A’(1, 11) maka:

2 + a = 1
a = -1 dan
4 + b = 11
b = 7
Titik B(x, y) memiliki bayangan B’(12, 13), maka:

x = 10 dan
y + 9 = 13
y = 4
Jadi, koordinat titik B adalah (10, 4)

2 + a = 1
a = -1 dan
4 + b = 11
b = 7
Titik B(x, y) memiliki bayangan B’(12, 13), maka:

x = 10 dan
y + 9 = 13
y = 4
Jadi, koordinat titik B adalah (10, 4)
Contoh soal 5 :
Garis yang persamaannya x – 2y + 3 = 0 ditransformasikan dengan transformasi yang berkaitan dengan matriks  . Persamaan bayangan garis itu adalah ...
. Persamaan bayangan garis itu adalah ...
 . Persamaan bayangan garis itu adalah ...
. Persamaan bayangan garis itu adalah ...Pembahasan :
Misalkan x = 1, maka 1 – 2y + 3 = 0 ==> -2y = -4, ==> y = 2 (maka titiknya (1, 2))
Misalkan x = 3, maka 3 – 2y + 3 = 0, ==> -2y = -6 ==> y = 3 (maka titiknya (3, 3))
Selanjutnya kita cari bayangan titik A(1, 2):

Bayangan titik A(1, 2) adalah A’(-5, -8)
Selanjutnya bayangan titik B(3, 3):

Bayangan titik B(3, 3) adalah B’(-6, -9)
Selanjutnya kita cari persamaan garis bayangannya, yaitu garis yang melalui titik A’(-5, -8) dan B’(-6, -9).
Masih ingatkah kalian rumus mencari persamaan garis yang melalui 2 titik? Yuk untuk mengingatkannya kalian boleh lihat disini:

-y – 8 = -x – 5
x – y = -5 + 8
x – y = 3
atau
x – y – 3 = 0
atau
-x + y + 3 = 0
Misalkan x = 3, maka 3 – 2y + 3 = 0, ==> -2y = -6 ==> y = 3 (maka titiknya (3, 3))
Selanjutnya kita cari bayangan titik A(1, 2):

Bayangan titik A(1, 2) adalah A’(-5, -8)
Selanjutnya bayangan titik B(3, 3):

Bayangan titik B(3, 3) adalah B’(-6, -9)
Selanjutnya kita cari persamaan garis bayangannya, yaitu garis yang melalui titik A’(-5, -8) dan B’(-6, -9).
Masih ingatkah kalian rumus mencari persamaan garis yang melalui 2 titik? Yuk untuk mengingatkannya kalian boleh lihat disini:

-y – 8 = -x – 5
x – y = -5 + 8
x – y = 3
atau
x – y – 3 = 0
atau
-x + y + 3 = 0
Contoh soal 6 :
Luas bayangan persegipanjang PQRS dengan
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
karena dilatasi [0,3] dilanjutkan rotasi pusat O bersudut π/2 adalah…
Pembahasan :
dilatasi [0,3] :
[O,3k] : P(x,y) → P ‘(3x, 3y)
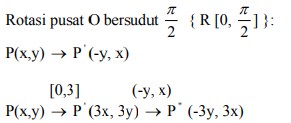
Sehingga :
P(x,y) → P” (-3y, 3x)
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
P(-1,2) → P” (-6,-3)
Q(3,2) → Q” (-6,9)
R (3,-1) → R” (3,9)
S(-1,-1) → S” (3,-3)
[O,3k] : P(x,y) → P ‘(3x, 3y)
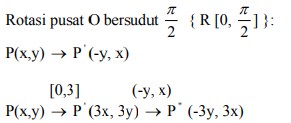
Sehingga :
P(x,y) → P” (-3y, 3x)
P(-1,2), Q(3,2), R (3,-1), S(-1,-1)
P(-1,2) → P” (-6,-3)
Q(3,2) → Q” (-6,9)
R (3,-1) → R” (3,9)
S(-1,-1) → S” (3,-3)
Buat sketsa gambarnya:
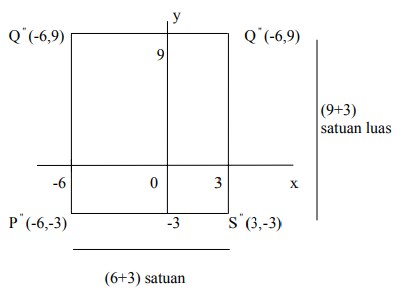
Sehingga luas transformasinya adalah :
Panjang (p) x lebar (l) = 12 x 9 = 108 satuan luas
Contoh soal 7 :
Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 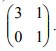 Luas bangun hasil transformasi segitiga ABC adalah….
Luas bangun hasil transformasi segitiga ABC adalah….
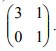 Luas bangun hasil transformasi segitiga ABC adalah….
Luas bangun hasil transformasi segitiga ABC adalah….Pembahasan :
misalkan T = 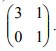 maka
maka
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3
luas ∆ ABC :
buat sketsa gambar :
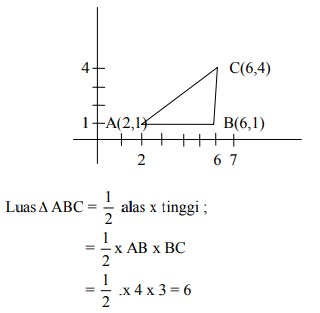
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC
= 3 x 6 = 18 satuan luas
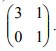 maka
makaLuas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3
luas ∆ ABC :
buat sketsa gambar :
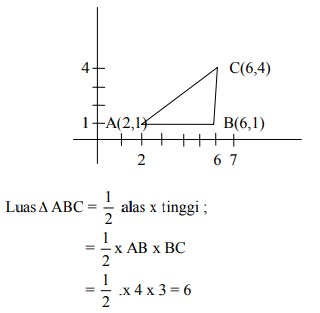
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC
= 3 x 6 = 18 satuan luas
Contoh soal 8 :
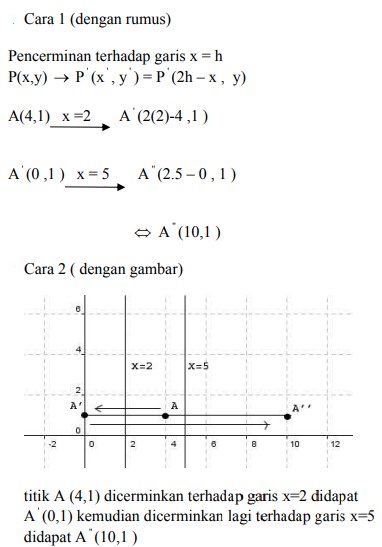
Bayangan titik A (4,1) oleh pencerminan terhadap garis x =2 dilanjutkan pencerminan terhadap garis x = 5 adalah titik….
Pembahasan :
Contoh soal 9 :
Segitiga ABC dengan A(2,1), B(6,1), C(6,4) ditransformasikan dengan matriks transformasi 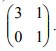 Luas bangun hasil transformasi segitiga ABC adalah….
Luas bangun hasil transformasi segitiga ABC adalah….
Pembahasan :
misalkan T = 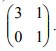 maka
maka
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC |det T| = |ad –bc| = |3-0| = 3
luas ∆ ABC :
buat sketsa gambar :
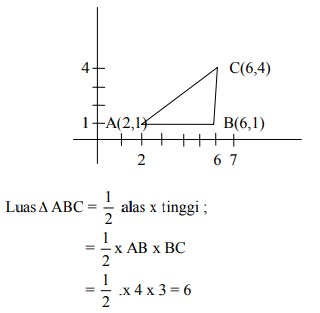
Luas bayangan/transformasi ∆ ABC =|det T| x luas ∆ ABC
= 3 x 6 = 18 satuan luas
Contoh soal 10 :
Jika titik A(15,8) dicerminkan terhadap garis x=7, maka bayangan titik A adalah titik A’ dengan koordinat….
Pembahasan : 
DAFTAR PUSTAKA
- https://www.ajarhitung.com/2017/08/contoh-soal-dan-pembahasan-tentang.html
- https://soalkimia.com/contoh-soal-transformasi-geometri/
Komentar
Posting Komentar