REMEDIAL PAS TRANSFORMASI MATRIKS

Nadia Nur Anggraini (28)
XI IPS 3

REMEDIAL PAS

28. Transformasi T adalah komposisi dari pencerminan terhadap garis y = x dilanjutkan rotasi dengan pusat O(0, 0) sebesar 90° dengan arah berlawanan arah putar jarum jam. Bayangan dari garis 3x + 5y − 2 = 0 oleh transformasi T mempunyai persamaan ....

Pembahasan :

$T_1=\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]$

$T_2=\left[\begin{array}{cc}cos{90}^{\circ }& -sin{90}^{\circ }\\ sin{90}^{\circ }& cos{90}^{\circ }\end{array}\right]=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]$

$T=\left[\begin{array}{cc}0& -1\\ 1& 0\end{array}\right]\left[\begin{array}{cc}0& 1\\ 1& 0\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]$

Bayangan titik (x, y) oleh transformasi T :
$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{c}x\\ y\end{array}\right]$

$\left[\begin{array}{c}{x}^{\prime }\\ y^{\prime }\end{array}\right]=\left[\begin{array}{c}-x\\ y\end{array}\right]$

Dari persamaan matriks diatas, diperoleh :
x' = -x  ↔  x = -x'
y' = y  ↔  y = y'

Substitusi x dan y ke persamaan kurva :
3x + 5y − 2 = 0
⇒  3(-x') + 5(y') − 2 = 0
⇔  -3x' + 5y' − 2 = 0
⇔  3x' − 5y' + 2 = 0

Jadi, persamaan bayangan kurva adalah :
3x − 5y + 2 = 0

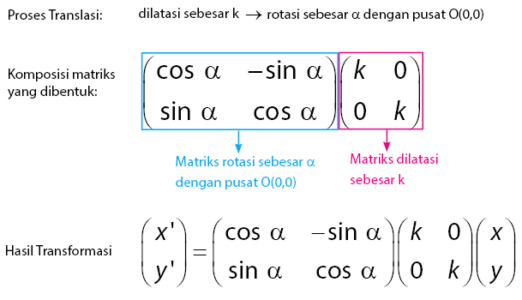
Proses menentukan hasil tranformasi dapat diperoleh melalui perkalian matriks yang mewakili matriks transformasi geometrinya. Namun, peletakan matriksnya berkebalikan dengan proses transformasinya. Misalkan sebuah transformasi geometri yang dinyatakan dalam dilatasi sebesar  dilanjutkan rotasi sebesar  dengan pusat . Maka persamaan perkalian matriks yang dibentuk adalah matriks rotasi sebesar  dengan pusat  dikali matriks dilatasi sebesar . Untuk lebih jelasnya perhatikan gambar di bawah.