PROGRAM LINEAR

NADIA NUR ANGGRAINI (28)

XI IPS 3

PROGRAM LINEAR

a. Pengertian

Program linear merupakan suatu program yang digunakan sebagai metode penentuan nilai optimum dari suatu persoalan linear. Nilai optimum (maksimal atau minimum) dapat diperoleh dari nilai dalam suatu himpunan penyelesaiaan persoalan linear.

Di dalam persoalan linear tersebut terdapat fungsi linear yang bisa disebut sebagai fungsi objektif. Persyaratan, batasan, dan kendala dalam persoalan linear adalah merupakan sistem pertidaksamaan linear.

b. Model Matematika Program Linear

Persoalan dalam program linear yang masih dinyatakan dalam kalimat-kalimat pernyataan umum, kemudian diubah kedalam model matematika. Model matematika merupakan pernyataan yang menggunakan peubah dan notasi matematika.

Sebagai ilustrasi, produsen sepatu membuat 2 model sepatu menggunakan 2 bahan yang berbeda. Komposisi model pertama terdiri dari 200 gr bahan pertama dan 150 gr bahan kedua. Sedangkan komposisi model kedua terdiri dari 180 gr bahan pertama dan 170 gr bahan kedua. Persediaan di gudang bahan pertama 72 kg dan bahan kedua 64 kg. Harga model pertama adalah Rp. 500.000,00 dan model kedua Rp. 400.000,00. Jika disimpulkan/disederhanakan dalam bentuk tabel menjadi berikut:

Dengan peubah dari jumlah optimal model 1 adalah x dan model 2 adalah y, dan hasil penjualan optimal adalah f(x, y) = 500.000x + 400.000y. Dengan syarat:

• Jumlah maksimal bahan 1 adalah 72.000 gr, maka 200x + 180y ≤ 72.000.
• Jumlah maksimal bahan 2 adalah 64.000 gr, maka 150x + 170y ≤ 64.000
• Masing-masing model harus terbuat.

Model matematika untuk mendapat jumlah penjualan yang maksimum adalah:

Maksimum f(x, y) = 500.000x + 400.000y

Syarat:

• 200x + 180y ≤ 72.000
• 150x + 170y ≤ 64.000
• x ≥ 0
• y ≥ 0

c. Cara Menyelesaikan Program Linear

Cara menyelesaikan masalah program linear bisa disebut sebagai sebuah proses guna mencari nilai optimum dari sebuah pertidaksamaan.

Nilai itu bisa berwujud nilai maksimum atau minimum, tergantung dengan soal yang akan diberikan. Bentuk umum fungsi objektif dari sebuah model matematika yaitu f(x,y) = ax + by.

Adapun dua metode yang bisa kita pakai untuk mencari menentukan nilai optimum pada program linear. Kedua metode tersebut adalah metode uji titik pojok dan garis selidik.

1. METODE UJI TITIK POJOK

Beberapa tahapan yang dilakukan untuk menentukan nilai optimum dengan menggunakan metode uji titik pojok yaitu sebagai berikut.

1. Mencari berbagai garis dari sistem pertidaksamaan yang menjadi fungsi kendala dari persoalan yang diberikan.
2. Mencari berbagai titik pojok yang merupakan koordinat pembatas daerah yang memenuhi fungsi kendala.
3. Menghitung nilai optimum f(x,y) dari titik-titik pojok yang diperoleh.
4. Memperoleh nilai maksimum atau minimum sesuai dengan permasalahan.

Contoh soal :

Apabila pada masing-maisng satu adonan kue basah bisa memberikan keuntungan Rp75.000,00 serta masing-masing adonan kue kering bisa memberikan untung Rp60.000,00. 

Sehingga, fungsi tujuannya yaitu memaksimalkan f(x,y) = 75.000x + 60.000y.

Menggambar daerah yang memenuhi pada sistem pertidaksamaan di atas.

Menentukan titik koordinat yang menjadi titik pojok pembatas daerah layak dari permasalahan sistem pertidaksamaan.

Titik Koordinat O, A, dan juga C bisa kita peroleh dengan cara melihat gambar di atas. Yakni dengan melihat O(0,0), A(0, 5), dan juga C(3, 0).

Sementara untuk koordinat titik B bisa kita peroleh dengan memanfaatkan metode eliminasi.

Untuk mencari koordinat titik B maka caranya adalah sebagai berikut:

x + y = 5

2x + y = 6
________ –
-x = -1
x = -1/-1 = 1

Substitusi nilai x = 1 pada persamaan x + y = 5 untuk memperoleh nilai y.

x + y = 5

1 + y  =5

y = 5 – 1 = 4

Koordinat titik B yaitu (1, 4)

Perhitungan nilai optimum:

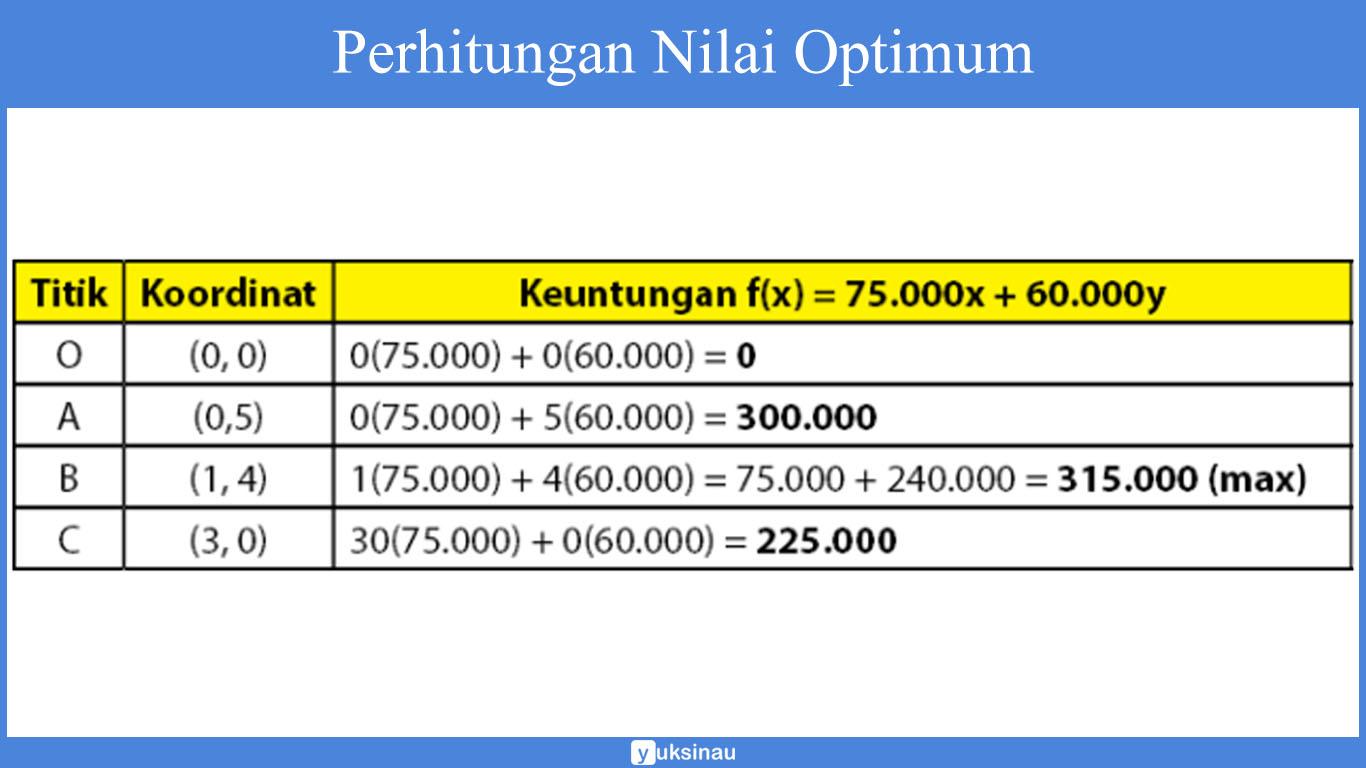
Sehingga, nilai keuntungan maksimum yang bisa didapatkan yaitu Rp315.000,00 dengan membuat 1 (satu) adonan roti basah dan juga 4 (empat) adonan roti kering.

2. METODE GARIS SELIDIK

Pada metode garis selidik, cara yang bisa digunakan untuk mencari nilai optimum yang didapatkan dari persamaan fungsi objektif atau fungsi tujuannya.

Apabila fungsi tujuannya yaitu memaksimalkan. Maka nilai optimum didapatkan dari titik yang paling akhir menyentuh garis selidik yang digeser ke arah kanan mendekati daerah layak.

Sementara untuk nilai optimum dengan fungsi tujuan meminimumkan akan didapatkan dari titik koordinat yang pertama kali menyentuh geseran garis selidik yang digeser ke arah kiri mendekati daerah layak.

Hal itu juga berlaku untuk sebaliknya.

Berikut ini merupakan tahapan untuk menentukan nilai optimum dari fungsi objektif f(x,y) = ax + by dengan menggunakan metode garis selidik :

1. Mencari daerah yang memenuhi sistem pertidaksamaan yang diberikan.
2. Mencari persamaan garis selidik f(x,y) = ax + by = k, dengan k merupakan bilangan real.
   Apabila arah geser garis selidik ke arah kanan maka:
   • Apabila titik (x1.y1) merupakan titik pada daerah penyelesaian yang pertama dilewati oleh garis selidik maka nilai minimum diwakili oleh titik tersebut.
   • Apabila titik (x2.y2) merupakan titik pada daerah penyelesaian yang terakhir dilewati oleh garis selidik maka nilai maksimum diwakili oleh titik tersebut.
     Geser garis selidik yang sudah dibikin pada langkah nomor 2 atau buatlah garis-garis lain yang sejajar dengan garis selidik yang sudah dibikin pada arah daerah layak.
Apabila arah geser garis selidik ke kiri, maka:
• Apabila titik (x1.y1) merupakan titik pada daerah penyelesaian yang pertama dilewati oleh garis selidik maka nilai maksimum akan diwakili oleh titik tersebut.
• apabila titik (x2.y2) merurpakan titik pada daerah penyelesaian yang terakhir dilewati oleh garis selidik maka nilai minimum diwakili oleh titik tersebut.

Contoh soal :

Apabila pada masing-maisng satu adonan kue basah bisa memberikan keuntungan Rp75.000,00 serta masing-masing adonan kue kering bisa memberikan untung Rp60.000,00. 

Sehingga, fungsi tujuannya yaitu memaksimalkan f(x,y) = 75.000x + 60.000y.

Persamaan garis selidik (ambil nilai k = 600.000):

f(x,y) = k

75.000x + 60.000y = 600.000

5x + 4y = 40

Menggambar daerah yang memenuhi sistem pertidaksamaan di atas serta garis selidiknya.

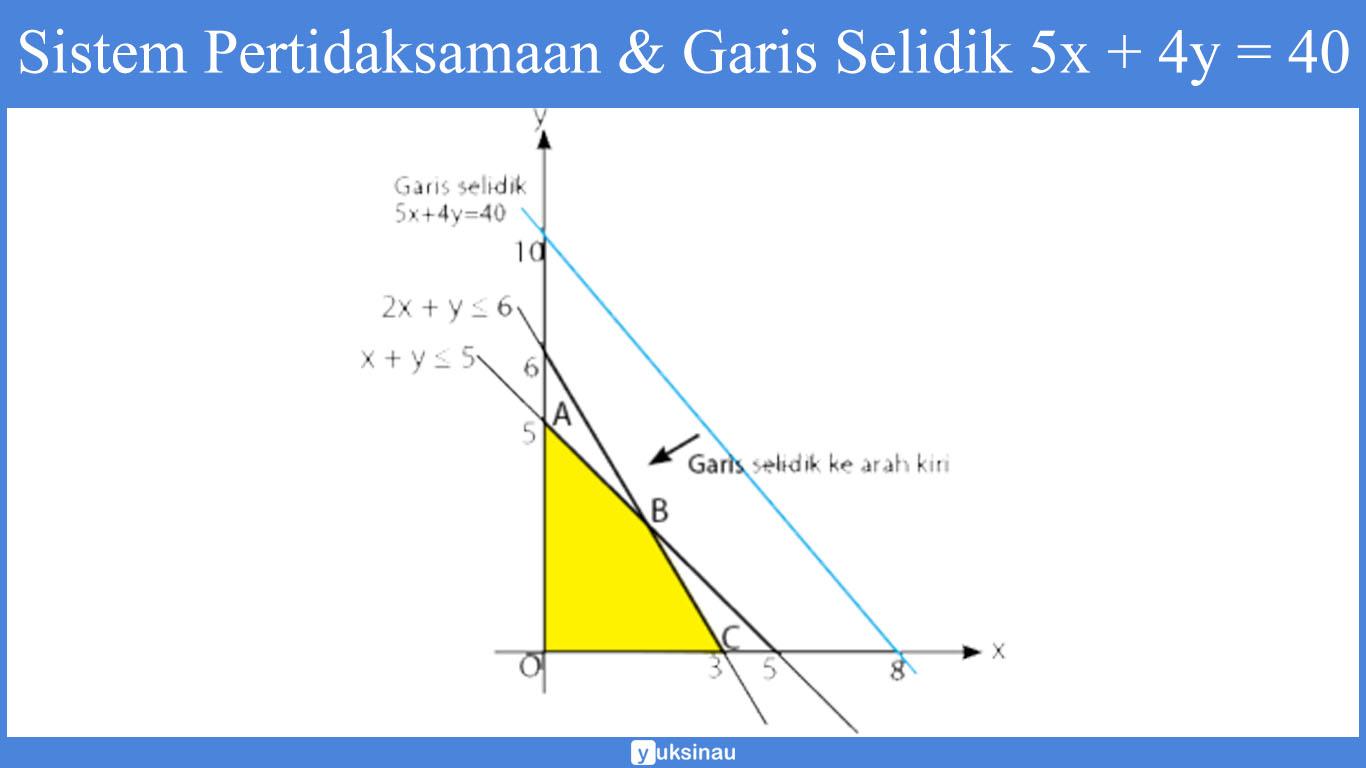
Nilai maksimum akan diwakili oleh titik B (titik yang pertama kali menyentuh garis selidik yang digeser ke arah kiri).
Mencari koordinat titik B dengan cara seperti berikut:

x + y = 5

2x + y = 6
________ –
-x = -1
x = -1/-1 = 1

Substitusi nilai x = 1 pada persamaan x + y = 5 untuk memperoleh nilai y.

x + y = 5

1 + y  =5

y = 5 – 1 = 4

Koordinat titik B yaitu (1, 4)

Substitusi koordinat titik B(1,4) pada persamaan f(x,y) = 75.000x + 60.000y.

f(x,y) = 75.000x + 60.000y

f(x,y) = 75.000(1) + 60.000y(4)

f(x,y) = 75.000 +240.000

f(x,y) = 315.000

Sehingga, nilai keuntungan maksimum yang bisa didapatkan yakni Rp315.000,00 dengan membuat 1 (satu) adonan roti basah serta 4 (empat) adonan roti kering.