MATRIK, MACAM-MACAM MATRIK DAN OPERASI MATRIK

Minggu, Agustus 30, 2020

Nama : Nadia Nur Anggraini
No absen : 28
Kelas : XI IPS 3

PENGERTIAN MATRIKS, MACAM - MACAM MATRIKS, OPERASI MATRIKS, DAN CONTOH SOALNYA

A. PENGERTIAN MATRIKS

Matriks adalah kumpulan bilangan yang disusun secara baris atau kolom atau kedua-duanya dan di dalam suatu tanda kurung. Bilangan-bilangan yang membentuk suatu matriks disebut sebagai elemen-elemen matriks. Matriks digunakan untuk menyederhanakan penyampaian data, sehingga mudah untuk diolah.

B. MACAM - MACAM MATRIKS

Matriks dapat dikelompokan ke beberapa jenis berdasarkan pada jumalah baris dan kolom serta pola elemen matriksnya sebagai berikut :

1. Matriks Baris dan Matriks Kolom

Matriks baris adalah suatu matriks yang hanya memiliki satu baris saja. Sedangkan, matriks kolom adalah suatu matriks yang hanya memiliki satu kolom saja.

Contoh: A = (1 4) atau B = (3 7 9) adalah matriks baris

$\begin{pmatrix} 146 \\ 275 \\ 528 \end{pmatrix}$ atau $D = \begin{pmatrix} p \\ q \end{pmatrix}$ adalah matriks kolom

2. Matriks Persegi

Matriks yang memiliki jumlah kolom dan baris yang sama disebut matriks persegi. Matriks persegi memiliki ordo n.

Contoh:

$A = \begin{pmatrix} 34 & 56 & 41 \\ 45 & 36 & 37 \\ 51 & 32 & 46 \end{pmatrix}$ adalah matriks persegi berordo 3, atau

$B = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}$ adalah matriks persegi berordo 2.

3. Matriks Segitiga Atas dan Segitiga Bawah

Matriks persegi A yang memiliki elemen matriks $a_{ij} = 0$ untuk $i > j$ atau elemen-elemen matriks dibawah diagonal utama bernilai 0 disebut matriks segitiga atas. Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i < j$ atau elemen-elemen matriks diatas diagonal utama bernilai 0 disebut matriks segitiga bawah.

Contoh:

$A = \begin{pmatrix} 1 & 6 & 4 \\ 0 & 3 & 7 \\ 0 & 0 & 4 \end{pmatrix}$ adalah matriks segitiga atas,

$B = \begin{pmatrix} 1 & 0 & 0 \\ 7 & 3 & 0 \\ 4 & 6 & 4 \end{pmatrix}$ adalah matriks segitiga bawah.

4. Matriks Diagonal

Matriks persegi A yang memiliki elemen matiks $a_{ij} = 0$ untuk $i \neq j$ atau elemen-elemen matriks diluar diagonal utama bernilai 0 disebut matriks diagonal.

Contoh:

$A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 4 \end{pmatrix}$ atau $B = \begin{pmatrix} 1 & 0 \\ 0 & 4 \end{pmatrix}$

5. Matriks Skalar

Matriks diagonal yang memiliki elemen-elemen pada diagonal utamanya bernilai sama disebut matriks skalar.

Contoh:

$A = \begin{pmatrix} 3 & 0 & 0 \\ 0 & 3 & 0 \\ 0 & 0 & 3 \end{pmatrix}$ atau $B = \begin{pmatrix} 4 & 0 \\ 0 & 4 \end{pmatrix}$

6. Matriks Indentitas

Matriks identitas ialah matriks yang diagonal utamanya selalu bernilai 1. Contohnya sebagai berikut :

7. Matriks Simetris

Matriks persegi A yang memiliki elemen matiks baris ke-I sama dengan elemen matriks kolom ke-j untuk i = j disebut simetris. Atau, dapat dikatakan elemen $a_{ij}$ sama dengan elemen $a_{ji}$ .

Contoh:

$\begin{pmatrix} 1 & 2 & 4 \\ 2 & 3 & 5 \\ 4 & 5 & 7 \end{pmatrix}$

Dapat dilihat bahwa elemen baris ke-1 sama dengan kolom ke-1, baris ke-2 sama dengan kolom ke-2, dan baris ke-3 sama dengan kolom ke-3.

C. OPERASI MATRIKS

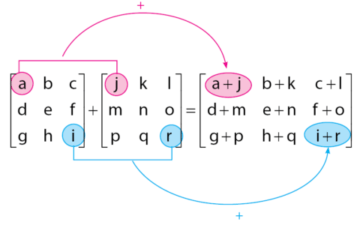
1. Penjumlahan Matriks

Syarat pada penjumlahan matriks ialah harus memiliki ordo yang sama, dan menambahkan pada posisi atau letak yang sama. Contohnya sebagai berikut :

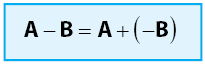
2. Pengurangan Matriks

Syarat pada pengurangan matriks juga sama dengan penjumlahan. Misal matriks C adalah pengurangan matriks A dan B, perlu kita ketahui bahwa matriks pengurangan ialah sama dengan penambahan Matriks A dengan perkalian skalar -1 dengan matriks B.

"C=A-B" sama dengan "C = A+ [-1] B"

Contoh pengurangan matriks sebagai berikut :

3. Perkalian Matriks

Operasi Hitung pada Matriks dan Sifat-sifatnya

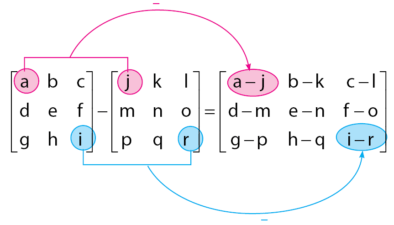
Perkalian Matriks dengan Skalar

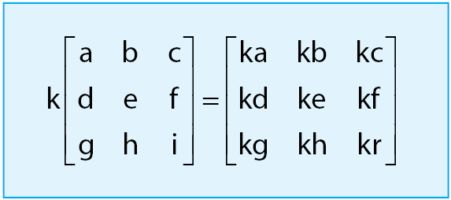
Pada perkalian matriks dengan skalar caranya yaitu mengalikan nilai skalar dengan semua letak matriks. Contohnya sebagai berikut :

Perkalian Matriks dengan Matriks

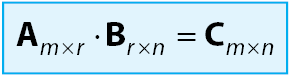
Syarat pada perkalian matriks ialah jumlah kolom pada matriks pertama sama dengan jumlah baris pada matriks kedua. Contohnya sebagai berikut perkalian A2x3 dan 3x3 :

D. CONTOH SOAL MATRIKS

Contoh soal 1 :

Diketahui matriks

. Nilai determinan dari matriks (AB – C) adalah ...

Pembahasan:

Det (AB – C) = (12.1) – (9.1) = 12 – 9 = 3

Jawaban : 3

Contoh soal 2 :

Diketahui matriks

, invers matriks AB adalah ...

Pembahasan:

Contoh soal 3 :

Matriks X yang memenuhi:

adalah ...

Pembahasan:

DAFTAR PUSTAKA

➟https://www.ajarhitung.com/2017/01/contoh-soal-dan-pembahasan-tentang_24.html

➟https://www.studiobelajar.com/matriks-dasar/

➟https://www.materipelajaran.web.id/2018/01/pengertian-matriks-jenis-dan-operasi-matriks.html

Cari Blog Ini

MATEMATIKA WAJIB